Is Bayesian inference subjective?
In a previous blog post (covering [1]) I discussed how inferential approaches to community detection are based on the formulation of generative models, via the definition of a likelihood \(P({\boldsymbol A}|{\boldsymbol b})\) for the network \({\boldsymbol A}\) conditioned on a partition \({\boldsymbol b}.\) With this at hand, we find the best partition of the network according to the posterior distribution, using Bayes' rule, i.e.
\[P({\boldsymbol b}|{\boldsymbol A}) = \frac{P({\boldsymbol A}|{\boldsymbol b})P({\boldsymbol b})}{P({\boldsymbol A})}, \tag{1}\]
where \(P({\boldsymbol b})\) is the prior probability for a partition \({\boldsymbol b}\).
In Bayesian statistics, probabilities are often described as representing a state of knowledge or even as quantification of a “personal belief” [2]. Does that mean that the results that we obtain using this method are “subjective,” and depend arbitrarily on how we choose our models and priors over parameters?
There’s an old debate in the statistics and philosophy literatures between “subjective” and “objective” Bayesianism, concerning primarily whether universal “non-informative” priors exist that perfectly represent the notion of maximum ignorance before any data is seen.1
1 The “subjective” position, as defended e.g. by de Finetti and Savage, argues simply that the postulates of inductive logic make no requirement on the prior distribution, which therefore needs to be chosen according to other criteria. The “objective” camp, represented most famously by Jeffreys and Janyes, argues in favor of additional postulates that enable the choice of universal “non-informative” priors. In the case of Jeffreys these are distributions invariant to reparametrization, and in Jaynes’ those derived according to the maximum entropy principle. Whether truly “non-informative” priors are indeed possible (they are not: the concept of “ignorance” does not exist in a vacuum and always requires initial choices on parametrization and constraints [3]) is not the main issue addressed in this post. See also footnote 3.
Regardless of the outcome of this debate, I think it is not very difficult to argue that the answer to the above question is “no” — at least when operating with the colloquial meaning of “subjective” as something that is based on or influenced by personal feelings, tastes, or opinions.
First, it is important to distinguish between the colloquial and a more technical definition of what constitutes a “subjective” statement. According to the more technical definition, we say that a statement is subjective when its veracity is conditioned on the subject that makes the statement, without necessarily meaning that the subject is free to decide on its veracity. A good example of this type of subjectivity is time in Einstein's theory of relativity: it has a subjective nature since it will be experienced differently depending on the frame of reference of the observer. Nevertheless, this does not mean that time can be freely determined by any observer, nor that it will be influenced by her personal feelings, tastes, or opinions. In other words, a subjective statement is not the same as an arbitrary statement. In this sense (and only in this sense), Bayesian statistics is indeed subjective, since an inferential conclusion will depend on the data observed and set of hypotheses considered by an individual. However, given the same data and set of hypotheses, two subjects must agree on the conclusion — it is not quite an arbitrary decision. In the colloquial sense of the term, Bayesian inference is not subjective.
There are different ways to demonstrate this more concretely. For example, we can argue “a la Jaynes” that a “state of knowledge” is not something arbitrary, since it can be quantified and always needs to be substantiated [4]. An alternative way of showing this, and which I find the most compelling, is via the equivalence between inference and compression. Namely, we can write the numerator of the posterior distribution of Equation 1 as
\[P({\boldsymbol A}|{\boldsymbol b})P({\boldsymbol b}) = 2^{-\Sigma({\boldsymbol A},{\boldsymbol b})},\]
where the quantity \(\Sigma({\boldsymbol A},{\boldsymbol b})\) is known as the description length [5] of the network. It is computed as:
\[\Sigma({\boldsymbol A},{\boldsymbol b}) = \underset{\mathcal{D}({\boldsymbol A}|{\boldsymbol b})}{\underbrace{-\log_2P({\boldsymbol A}|{\boldsymbol b})}}\, \underset{\mathcal{M}({\boldsymbol b})}{\underbrace{- \log_2P({\boldsymbol b})}}. \tag{2}\]
The second term \(\mathcal{M}({\boldsymbol b})\) in the above equation quantifies the amount of information in bits necessary to encode the parameters of the model, while the first term \(\mathcal{D}({\boldsymbol A}|{\boldsymbol b})\) determines how many bits are necessary to encode the data (the observed network itself), once the model parameters are known. Therefore, finding the most likely network partition is equivalent to finding the one that most compresses it — giving us a compelling implementation of Occam's razor.2
2 An important technical remark is that Equation 2 only corresponds to an actual description length if the quantities involved are probability mass functions, i.e. the set of possible data and parameters are discrete. This is not a limitation of the framework, it only embodies the unavoidable fact that we can only extract finite information from data. Hypotheses defined over continuous parameters need either to be marginalized or discretized within a finite precision in order to be converted into specific inferential statements.
The description length is not arbitrary in any way; in fact it is says something almost physical about the data. It means that if we infer the most likely model, it gives us a way of storing the data in a hard drive using \(\Sigma({\boldsymbol A},{\boldsymbol b})\) bits! As we know from our daily computer usage, compression is not an arbitrary decision, nor is it influenced by our personal feelings, tastes, or opinions — otherwise we would never run out of disk space, we would be able to download files instantly, etc. In other words, we cannot arbitrarily choose which model best fits the data in the same manner we cannot choose to make our computer files arbitrarily small. If we would accept that Bayesian statistics is arbitrary, then we would need also to accept that these physical obstacles we face are also arbitrary in nature, which is a rather absurd proposition, and demonstrably incorrect.
As I discussed previously, seeking compression avoids overfitting the data since it’s not possible (asymptotically) to compress statistical noise.
However, the concept of compression is more generally useful than just avoiding overfitting within a class of models. In fact, the description length gives us a model-agnostic objective criterion to compare different hypotheses for the data generating process according to their plausibility — in a manner that is not only not arbitrary but also not subjective. Namely, since Shannon's theorem tells us that the best compression can be achieved asymptotically only with the true data generating model, then if we are able to find a description length for a network using a particular model, regardless of how it is parametrized, this also means that we have automatically found an upper bound on the optimal compression achievable. By formulating different generative models and computing their description length, we have not only an objective criterion to compare them against each other, but we also have a way to limit further what can be obtained with any other model. The result is an universal scale on which different models can be compared, as we move closer to the limit of what can be uncovered for a particular data at hand.3
3 Note that the existence of this universal scale is othogonal to the debate on whether it is possible to define universal “non-informative” priors. Even if the choice of model and prior is arbitrary, its resulting compression of the data will not be.
In the figure below we show the description length values with some models obtained for a protein-protein interaction network for the organism Meleagris gallopavo (wild turkey).
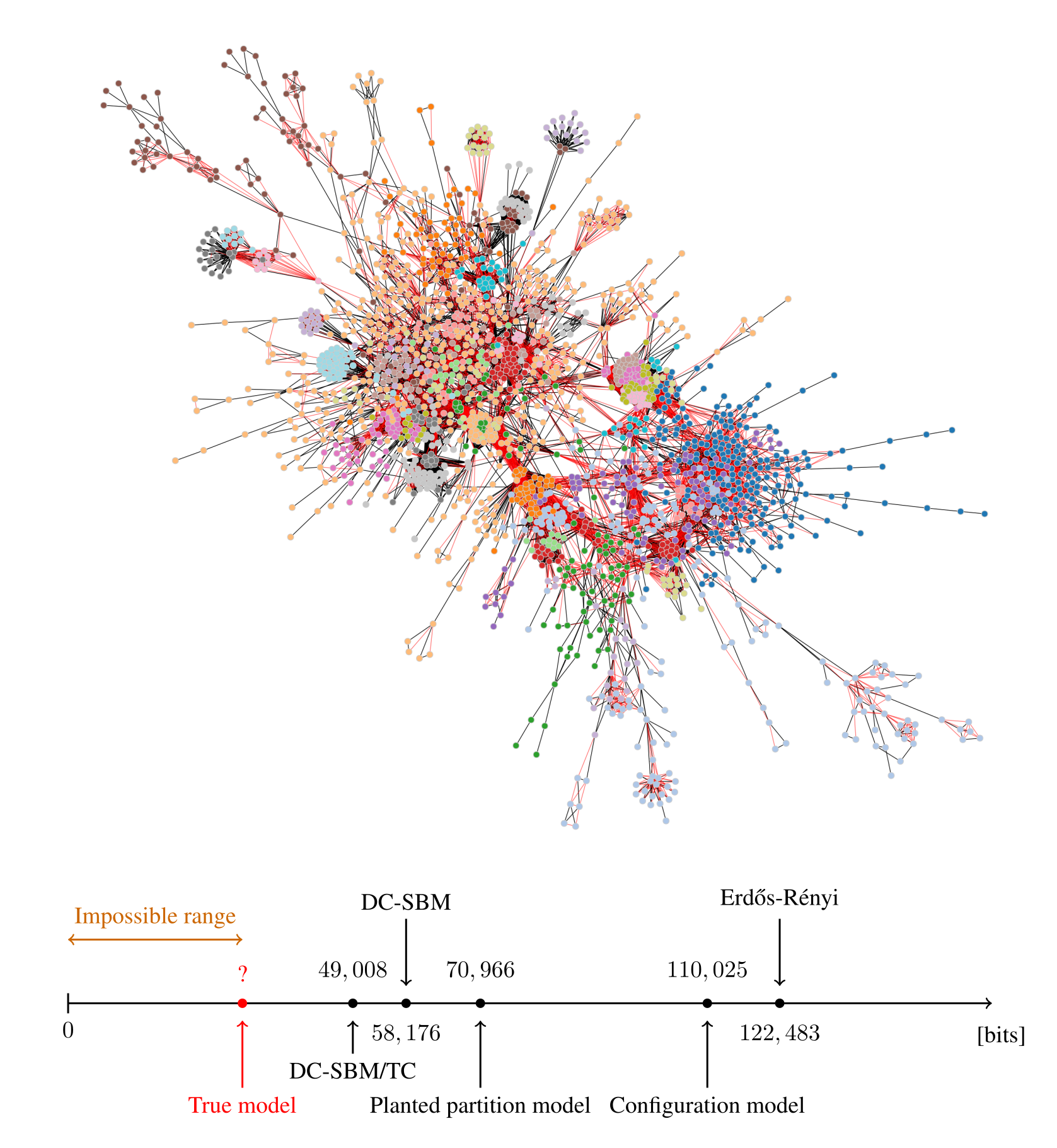
4 In an absolute sense, the true model is not only unkonwn, but also unknownable. What Figure 1 shows is that our task to appoximate it asymptotically.
In particular, we can see that with the degree-corrected stochastic block model with triadic closure (DC-SBM/TC) [6] we can achieve a description length that is far smaller than what would be possible with networks sampled from either the Erdős–Rényi, configuration, or planted partition (a SBM with strictly assortative communities [7] models, meaning that the inferred model is much closer to the true process that actually generated this network than the alternatives. Naturally, the actual process that generated this network is different from the DC-SBM/TC, and it likely involves, for example, mechanisms of node duplication which are not incorporated into this rather simple model. However, to the extent that the true process leaves statistically significant traces in the network structure,5 computing the description length according to it should provide further compression when compared to the alternatives. Therefore, we can try to extend or reformulate our models to incorporate features that we hypothesize to be more realistic, and then verify if this in fact the case, knowing that whenever we find a more compressive model, it is moving closer to the true one — or at least to what remains detectable from it for the finite data.
5 Visually inspecting Figure 1 reveals what seems to be local symmetries in the network structure, presumably due to gene duplication. These patterns are not exploited by the SBM description, and points indeed to a possible path for further compression.
The discussion above glosses over some important technical aspects. For example, it is possible for two (or, in fact, many) models to have the same or very similar description length values. In this case, Occam's razor fails as a criterion to select between them, and we need to consider them collectively as equally valid hypotheses. This means, for example, that we would need to average over them when making specific inferential statements [8] — selecting between them arbitrarily can be interpreted as a form of overfitting. Furthermore, there is obviously no guarantee that the true model can actually be found for any particular data. This is only possible in the asymptotic limit of “sufficient data”, which will vary depending on the actual model. Outside of this limit (which is the typical case in empirical settings, in particular when dealing with sparse networks), fundamental limits to inference are unavoidable, which means in practice that we will always have limited accuracy and some amount of error in our conclusions. However, when employing compression, these potential errors tend towards overly simple explanations, rather than overly complex ones. Whenever perfect accuracy is not possible, it is difficult to argue in favor of a bias in the opposite direction.
I emphasize that it is not possible to “cheat” when doing compression. For any particular model, the description length will have the same form
\[\Sigma(\boldsymbol A,\boldsymbol \theta) = \mathcal{D}(\boldsymbol A|\boldsymbol\theta) + \mathcal{M}(\boldsymbol \theta),\]
where \(\boldsymbol \theta\) is some arbitrary set of parameters. If we constrain the model such that it becomes possible to describe the data with a number of bits \(\mathcal{D}(\boldsymbol A|\boldsymbol \theta)\) that is very small, this can only be achieved, in general, by increasing the number of parameters \(\boldsymbol\theta\), such that the number of bits \(\mathcal{M}(\boldsymbol\theta)\) required to describe them will also increase. Therefore, there is no generic way to achieve compression that bypasses actually formulating a meaningful hypothesis that matches statistically significant patterns seen in the data.
One may wonder, therefore, if there is an automatized way of searching for hypotheses in a manner that guarantees optimal compression. The most fundamental way to formulate this question is to generalize the concept of minimum description length as follows: for any binary string \(\boldsymbol x\) (representing any measurable data), we define \(L(\boldsymbol x)\) as the length in bits of the shortest computer program that yields \(L(\boldsymbol x)\) as an output. The quantity \(L(\boldsymbol x)\) is know as Kolmogorov complexity, and if we would be able to compute it for a binary string representing an observed network, we would be able to determine the “true model” value in Figure 1, and hence know how far we are from the optimum.6
6 As mentioned before, this would not necessarily mean that we would be able to find the actual true model in a practical setting with perfect accuracy, since for a finite \(\boldsymbol x\) there could be many programs of the same minimal length (or close) that generate it.
7 There are two famous ways to prove this. One is by contradiction: if we assume that we have a program that computes \(L(\boldsymbol x)\), then we could use it as subroutine to write another program that outputs \(\boldsymbol x\) with a length smaller than \(L(\boldsymbol x)\). The other involves undecidabilty: if we enumerate all possible computer programs in order of increasing length and check if their outputs match \(\boldsymbol x\), we will eventually find programs that loop indefinitely. Deciding whether a program finishes in finite time is known as the “halting problem”, which has been proved to be impossible to solve. In general, it cannot be determined if a program reaches an infinite loop in a manner that avoids actually running the program and waiting for it to finish. Therefore, this rather intuitive algorithm to determine \(L(\boldsymbol x)\) will not necessarily finish for any given string \(\boldsymbol x\). For more details the wikipedia page has a good overview.
Unfortunately, an important result in information theory is that \(L(\boldsymbol x)\) is not computable. This means that it is strictly impossible to write a computer program that computes \(L(\boldsymbol x)\) for any string \(\boldsymbol x\).7 This is a rather counterintuitive and frustrating fact that means that while we can keep trying, and maybe eventually even succeeding in compressing some data better than our last attempt, whether we have at any point achieved the optimal compression will remain forever unknowable.
Some interpret the uncomputability of Kolmogorov complexity as an invalidation of the overall compression approach to model selection, but I think this is fundamentally mistaken. This fact simply means that we cannot automate the discovery of optimal hypotheses, or know where the “finish line” is. However, compression is still a perfectly valid and objective criterion to judge the relative plausibility of competing hypotheses. This is really the best we can hope for, and there’s an upside: It means that scientists will never run out of things to do, and their capacity for creativity in formulating new hypotheses will never become obsolete!
References
Webmentions8
(Nothing yet)
8 Webmention is a standardized decentralized mechanism for conversations and interactions across the web.
Comments
(Comments may be moderated.)
If you reply to this post, it will show as a comment below the original article.