Inferential network science
The 21st century has been marked by the unprecedented volume of digital data being increasingly produced on human behavior, biological organisms, economies, and a variety of other complex systems.
Networks delineate the constituent interactions of a broad range of such large-scale complex systems. They provide an essential mathematical representation of socio-economical relations, the human brain, cell metabolism, ecosystems, epidemic spreading, informational infrastructure, transportation systems, and many more.
The structure of these network systems is typically large and heterogeneous, and the interactions they describe are often non-linear, and result in nontrivial emergent behavior and self-organization.
Although network theory offers a wide ranging foundation to untangle such intricate systems, potentially allowing us to predict and control their behavior, the analysis of network data is particularly challenging. Since networks are high-dimensional relational objects, low-order statistics can reveal only very little about them. Conversely, higher-order representations are prone to overfitting, if obtained heuristically, and can easily yield misleading characterizations and statistical illusions.
Such a framework should be able to extract from data the most appropriate level of complexity that can be justified from statistical evidence, taking into account both epistemic and aleatoric uncertainty, while achieving interpretability, algorithmic efficiency, and versatility.
A central concern of ours is the practical implementation of inductive reasoning and statistical inference to relational data that come from a variety of complex systems in the real world. A lot of what we do is framed by the following instrumental questions:
- How do we prevent overfitting and produce explanations of empirical observations that correctly separate structure from randomness?
- How can we reconstruct dynamical rules and network structures from indirect information on their behavior?
- How do we faithfully model the hierarchical, modular, higher-order, and dynamical structure of network systems?
This line of work was recognized with the Erdős–Rényi Prize from the Network Science Society.
Most of the methods developed in our group are made available as part of the graph-tool library, which is extensively documented.
For a practical introduction to many inference and reconstruction algorithms, please refer to the HOWTO.
Simplicity science for complex systems
(or, from complex visibles to simple invisibles)
The essential goal of science is to find understandable explanations (inferred and sufficiently simple) to what at first seems incomprehensible behavior (observed and initially complex).1
1 Recommended: M. Marsili, Simplicity Science, Indian Journal of Physics 98, 3789 (2024).
In the context of complexity and network science, the understandable explanations that we seek are the fundamental local interaction rules that give rise to global emergent behavior. These fundamental rules are rarely observed directly—instead, they are almost always latent, i.e. hidden from the observer.
Therefore, to fulfill our scientific goal we must develop a robust inductive framework to infer the hidden minimal rules that govern complex behavior.
Structure vs. randomness
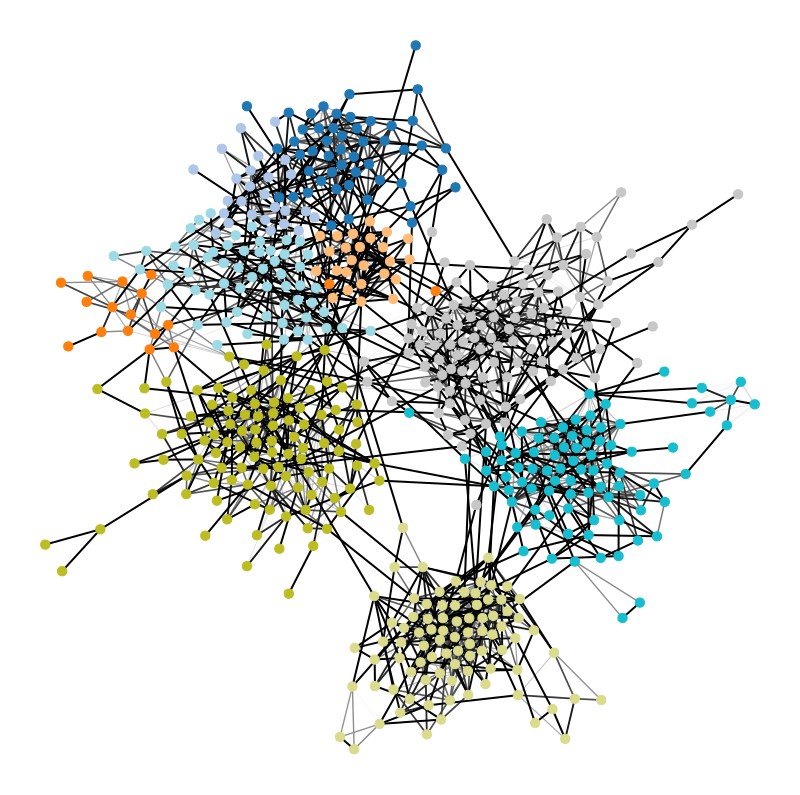
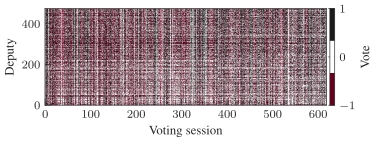
A significant obstacle for the inference of such high-dimensional relational objects lies in discerning between signal and randomness. We need to be able to identify which aspects of these systems arise from random stochastic fluctuations and which convey valuable information about an underlying phenomenon. This is a multifaceted problem that often defies intuition, and lies at the heart of any data-driven analysis.
Figure 1 below demonstrates how easy it is to mistake pure randomness for seemingly meaningful structure in complex systems.

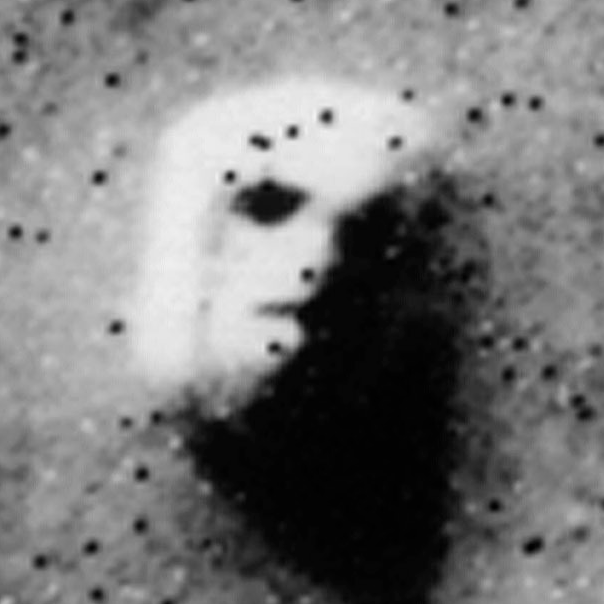

In our group, we focus on the development of principled and trustworthy methods to extract scientific understanding from network data, in a manner that avoids statistical illusions.
Our methods are designed to be robust against overfitting, honoring the principle of maximum parsimony—or Occam’s razor, as well as to enable model comparison, validation, and uncertainty quantification, while also being algorithmically efficient. This is achieved by merging analytical tools and concepts from a variety of disciplines, including Information Theory, Bayesian Statistics, Machine Learning, and Statistical Mechanics.
Network reconstruction
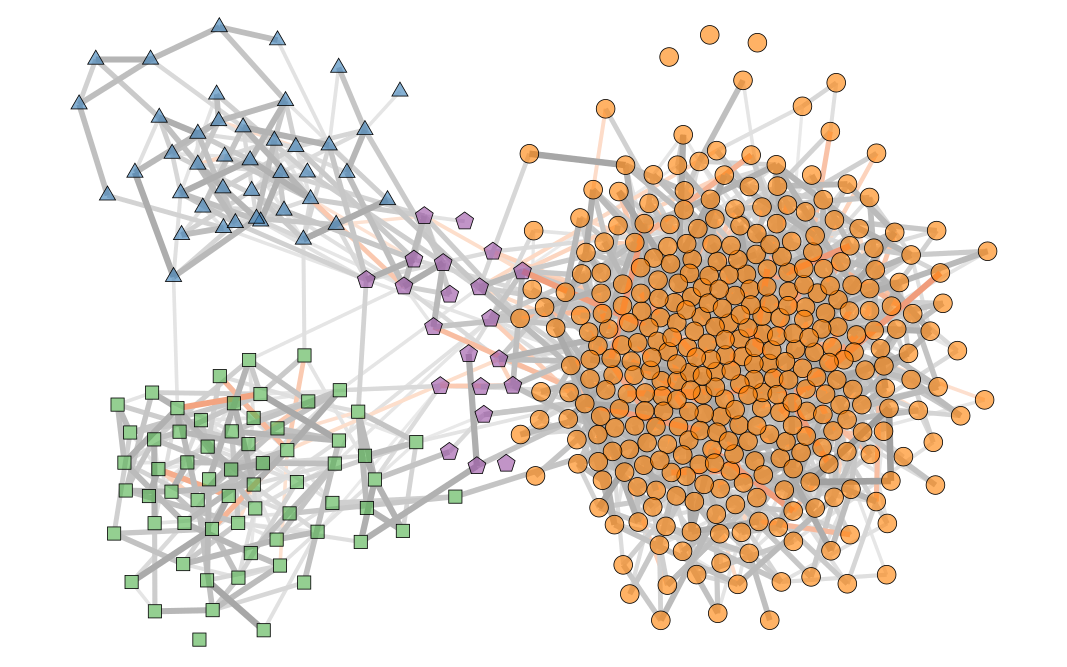
We’re particularly interested in problems of network inference where meaningful structural and functional patterns cannot be obtained by direct inspection or low-order statistics, and require instead more sophisticated approaches based on large-scale generative models and efficient algorithms derived from them. In more demanding, but nonetheless ubiquitous scenarios, the network data are noisy, incomplete, or even completely hidden, leaving their trace only via an observed dynamical behavior—in which case the network needs to be fully reconstructed from indirect information (see Figure 2) [1].
Research highlights
Inferring modular structures in networks
Annotated and attributed networks

Dynamical networks
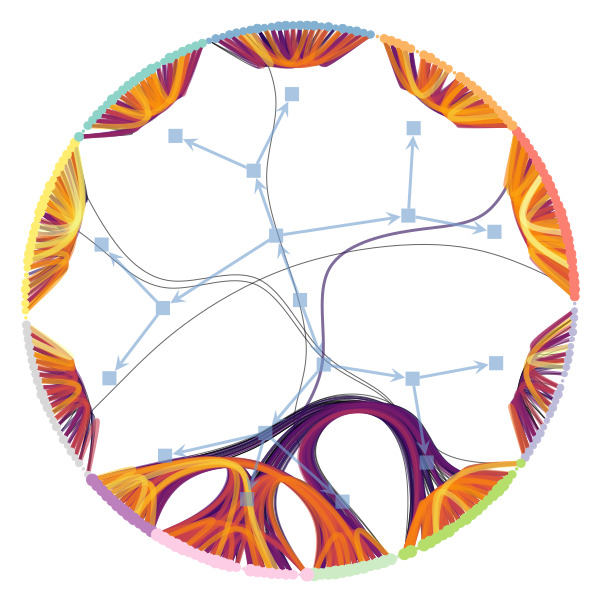





Uncertain network reconstruction
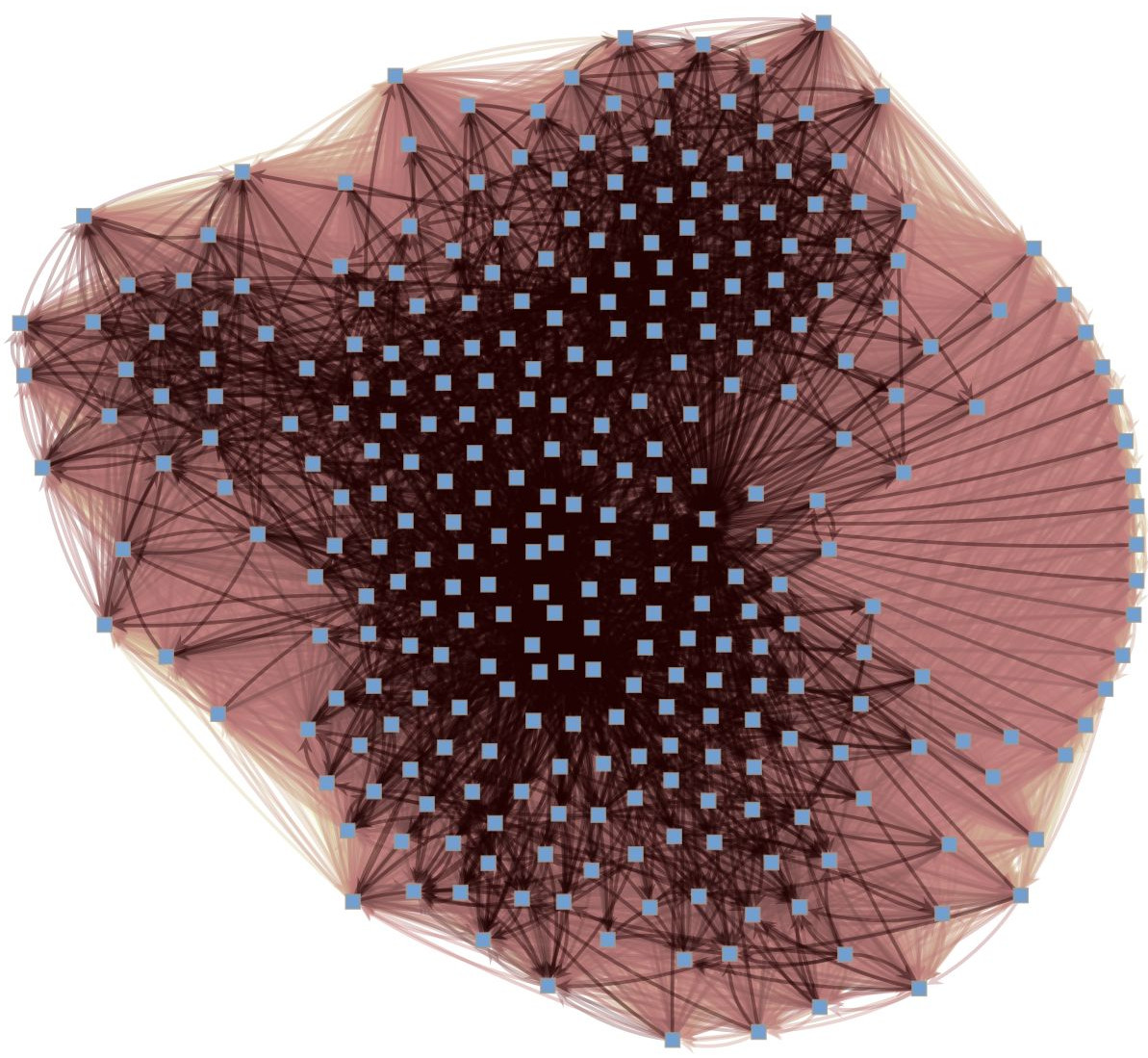
Reconstruction from dynamics
Disentangling edge formation mechanisms