Significant community structure via statistical tests?

This post is a slightly modified version of Sec. IVC in  [1].

In a previous blog post I explained how modularity maximization tends to overfit and find spurious community structure even in random graphs.

Sometimes practitioners are indeed aware that such non-inferential methods can find communities that are not supported by statistical evidence. In an attempt to extract an inferential conclusion from their results in spite of this, they compare the value of the quality function with a randomized version of the network — and if a significant discrepancy is found, they conclude that the community structure is statistically meaningful. Unfortunately, this approach is as fundamentally flawed as it is straightforward to implement.

The reason why the test fails is because in reality it answers a question that is different from the one intended. When we compare the value of the quality function (or any other test statistic) obtained from a network and its randomized counterpart, we can use this information to answer only the following question:

“Can we reject the hypothesis that the observed network was sampled from a random null model?”

No other information can be obtained from this test, including whether the network partition we obtained is significant. All we can determine is if the optimized value of the quality function is significant or not. The distinction between the significance of the quality function value and the network partition itself is subtle but crucial.

We illustrate the above difference with an example in Figure 1 (b). This network is created by starting with a fully random Erdős-Rényi (ER) network, and adding to it a few more edges so that it has an embedded clique of six nodes. The occurrence of such a clique from an ER model is very unlikely, so if we perform a statistical test on this network that is powerful enough, we should be able to rule out that it came from the ER model with good confidence. Indeed, if we use the value of maximum modularity for this test, and compare with the values obtained for the ER model with the name number of nodes and edges (see Figure 1 (a)), we are able to reach the correct conclusion that the null model should be rejected, since the optimized value of modularity is significantly higher for the observed network.

Figure 1: The statistical significance of the maximum modularity value is not informative of the significance of the community structure. In (a) we show the distribution of optimized values of modularity for networks sampled from the Erdős-Rényi (ER) model with the same number of nodes and edges as the network shown in (b) and (c). The vertical line shows the value obtained for the partition shown in (b), indicating that the network is very unlikely to have been sampled from the ER model (\(P = 0.002\)). However, what sets this network apart from typical samples is the existence of a small clique of six nodes that would not occur in the ER model. The remaining communities found in (b) are entirely meaningless. In (c) we show the result of inferring the stochastic block model on this network, which perfectly identifies the planted clique without overfitting the rest of the network.

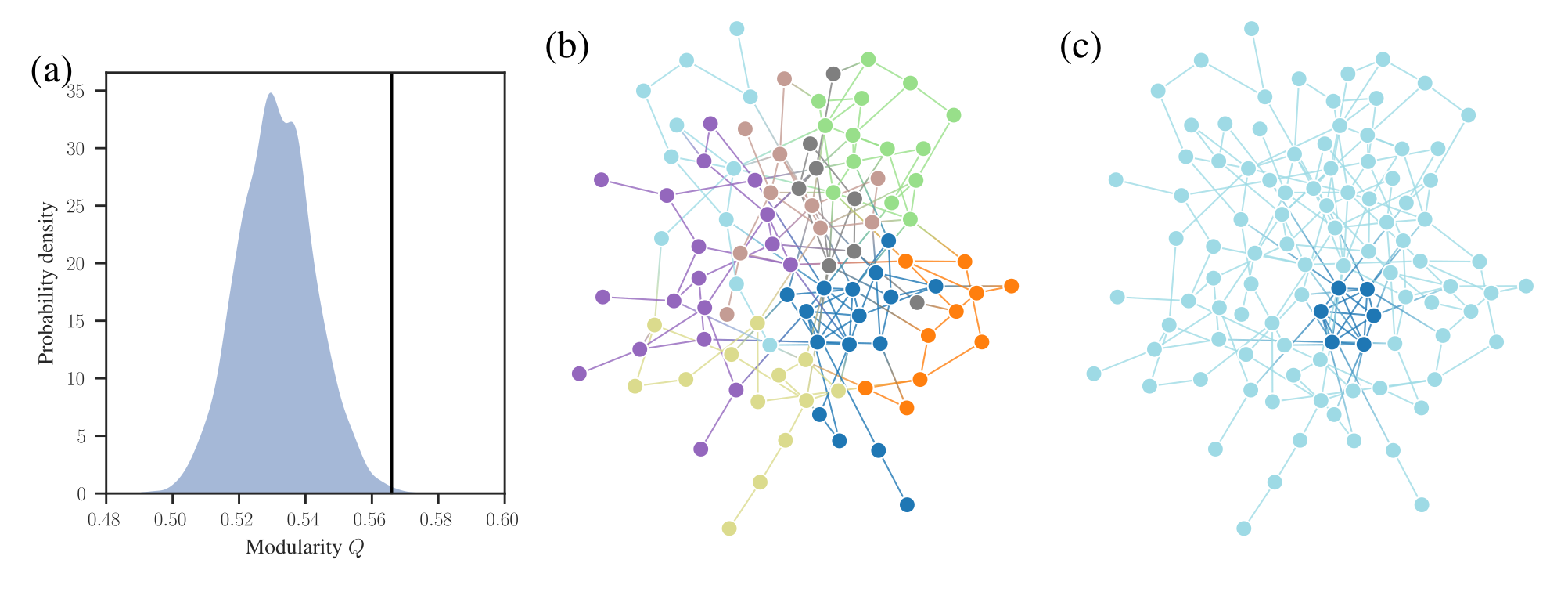
Should we conclude therefore that the communities found in the network are significant? If we inspect Figure 1 (b), we see that the maximum value of modularity indeed corresponds to a more-or-less decent detection of the planted clique. However, it also finds another seven completely spurious communities in the random part of the network. What is happening is clear — the planted clique is enough to increase the value of \(Q\) such that it becomes a suitable test to reject the null model¹, but the test is not powerful enough to verify that the communities themselves are statistically meaningful. In short, the following two statements are not synonymous:

¹ Note that it is possible to construct alternative examples, where instead of planting a clique, we introduce the placement of triangles, or other features that are known to increase the value of modularity, but that do not correspond to an actual community structure.

1. The maximum value of \(Q\) is significant.
2. The corresponding network partition is significant.

Conflating the two will lead to the wrong conclusion about the significance of the communities uncovered.

In Figure 1 (c) we show the result of a more appropriate inferential approach, based on Bayesian inference as described in a previous blog post, that attempts to answer a much more relevant question: “which partition of the network into groups is more likely?” The result is able to cleanly separate the planted clique from the rest of the network, which is grouped into a single community.

This example also shows how the task of rejecting a null model is very oblique to Bayesian inference of generative models. The former attempts to determine what the network is not, while the latter what it is. The first task tends to be easy — we usually do not need very sophisticated approaches to determine that our data did not come from a null model, specially if our data is complex. On the other hand, even if approximative, the second task is far more revealing, constructive, and arguably more useful in general.

References

[1]

T. P. Peixoto, Descriptive Vs. Inferential Community Detection in Networks: Pitfalls, Myths and Half-Truths, Elements in the Structure and Dynamics of Complex Networks (2023).

---

Comments

Webmentions²

(Nothing yet)

² Webmention is a standardized decentralized mechanism for conversations and interactions across the web.